本内容是《统计学习方法》(第2版)中的第二章,可以与第七章中的支持向量机(SVM)相结合进行学习。
一、感知机模型
感知机是一种二分类的线性模型,该方法对所分类的数据要求非常严格,数据必须是线性可分的,否则无法对其进行二分类,这对生活所遇到的数据来说是一项即为严格的条件,因此在使用感知机对数据进行二分类时,一定要确认数据是否是线性可分的。
感知机的数学定义为:
假设输入空间(特征空间)\({\cal{X}} \subseteq R^n\),输出空间是\(\cal{Y}=\{+1, -1\}\)。输入\(x\in \cal{X}\)表示实例的特征向量,对应于输入空间的(特征空间)的点;输出\(\cal{y}\in \cal{Y}\)表示实例的类别。由输入空间到输出空间的如下函数: \(f(x)=sign(w \cdot x+b)\) 称为感知机。其中,\(w\)和\(b\)为感知机参数,\(w\in R^n\)叫做权值或者权值向量,\(b\in R\)叫作偏置。\(w \cdot x\)表示\(w\)和\(x\)的內积。\(sign\)是符号函数。
感知机的几何表示如下
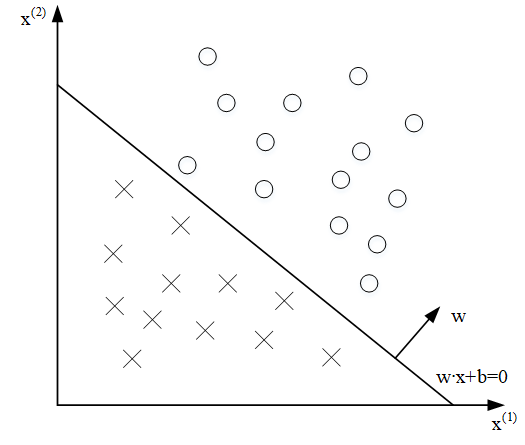
从这个几何表示中可以看出,对于线性可分的数据集,我们可以找到一个超平面\(S\)对数据集进行二分类;对于线性不可分的数据集是不能进行二分类的,例如对于异或运算,不能找到一个平面将这两类点进行分类。
二、感知机学习策略
2.1 感知机学习算法的原始形式
首先,我们根据感知机的几何表示,可以容易得到输入空间\(R^n\)中任一点\(x_0\)到超平面的距离为
\[\begin{aligned} \frac{1}{||w||}|w \cdot x_0+b| \end{aligned}\]对于误分类的点\((x_i,y_i)\)来说,其到超平面的距离就是
\[-\frac{1}{||w||} y_i(w \cdot x_i+b)\]因此在给定数据集\(\{T=\{(x_1,y_1),(x_2,y_2),...,(x_N,y_N)\}\}\), 其中\(x_i \in R^n\),\(y_i \in \{+1,-1\}\),\(i=1,2,...,N\),感知机学习的损失函数定义为
\[{\cal{L}}(w,b)=-\sum_{x_i \in M}y_i(w \cdot x_i+b)\]其中\(M\)为误分类点的集合,与误分类点到超平面的距离不同的是,这里缺少了\(\frac{1}{\Vert w \Vert}\),由于这一项可以认为是一个常数项,因此可以忽略,同时为了方面计算,我们往往会选取一个单位向量作为这个超平面的法向量。
有了上面的损失函数,我们就可以将求感知机模型参数\(w,b\)的问题表示为如下的最优化问题
\[\min_{w,b}{\cal{L}}(w,b)=-\sum_{x_i\in M} y_i(w\cdot x_i+b)\]针对上述的损失函数极小化问题,可以采用随机梯度下降法。首先,任意选择一个超平面\(w_0,b_0\),然后用梯度下降法不断地极小化目标函数,极小化过程中不是一次对所有误分类的点的梯度下降,而是一次随机选取一个误分类点使其梯度下降。可以得到损失函数\(\cal{L}\)对\(w\)与\(b\)的梯度分别为
\[\begin{aligned} \nabla _w {\cal{L}}(w,b) &= -\sum_{x_i\in M}y_ix_i\\ \nabla _b {\cal{L}}(w,b) &= -\sum_{x_i\in M}y_i \end{aligned}\]因此对于误分类点\((x_i,y_i)\),对\(w,b\)进行更新:
\[\begin{aligned} w &\leftarrow w+\eta y_i x_i\\ b &\leftarrow b+\eta y_i \end{aligned}\]其中\(\eta(0< \eta\le1)\)是步长,也称为学习率。这样通过多次迭代,就可以得到使损失函数不断减小,直到为0。因此也就可以得到感知机学习算法的原始形式
输入:训练数据集\(\{T=\{(x_1,y_1),(x_2,y_2),...,(x_N,y_N)\}\}\), 其中\(x_i \in R^n\),\(y_i \in \{+1,-1\}\),\(i=1,2,...,N\);学习率\(\eta(0< \eta\le1)\);
输出:\(w,b\);感知机模型\(f(x)=sign(w \cdot x+b)\)。
(1)选取初值\(w_0,b_0\);
(2)在训练集中选取数据\((x_i,y_i)\);
(3)如果\(y_i(w \cdot x_i+b)\le0\),
\[\begin{aligned} w &\leftarrow w+\eta y_i x_i\\ b &\leftarrow b+\eta y_i \end{aligned}\](4)转至(2),直至训练集中没有误分类点。
2.2 感知机算法的对偶形式
对偶形式的基本想法是,将\(w\)和\(b\)表示为实例\(x_i\)和标记\(y_i\)的线性组合的形式,通过求解其系数而求得\(w\)和\(b\)。当学习率\(\eta\)选定了之后,模型参数\(w,b\)每次的增量是固定的,分别为\(\eta y_i x_i\)与\(\eta y_i\)。因此对于误分类点\((x_i,y_i)\),参数\(w,b\)修改了\(n_i\)次,则参数关于该误分类点的增量就为\(\alpha_i y_i x_i\)和\(\alpha_i y_i\),其中\(\alpha_i=n_i\eta\)。由于参数的初始值可以任意设定,因此为了便于计算和表示,设置\(w_0,b_0\)均为0,则最终学习到的参数\(w,b\)为
\[\begin{aligned} w &=\sum_{i=1}^N\alpha _i y_i x_i\\ b &=\sum_{i=1}^N\alpha _i y_i \end{aligned}\]其中\(\alpha _i \ge0,i=1,2,...,N\)。与感知机算法的原始形式相似,可以得到感知机算法的对偶形式:
输入:训练数据集训练数据集\(\{T=\{(x_1,y_1),(x_2,y_2),...,(x_N,y_N)\}\}\), 其中\(x_i \in R^n\),\(y_i \in \{+1,-1\}\),\(i=1,2,...,N\);学习率\(\eta(0< \eta\le1)\);
输出:\(\alpha,b\);感知机模型\(f(x)=sign(\sum_{j=1}^N\alpha _j y_j x_j \cdot x+b)\),其中\(\alpha =(\alpha_1,\alpha_2,...,\alpha_N)^T\)。
(1)\(\alpha \leftarrow 0, b \leftarrow 0\);
(2)在训练集中选取数据\((x_i,y_i)\);
(3)如果\(y_i(\sum_{j=1}^N\alpha _j y_j x_j \cdot x_i+b)\le0\),
\[\begin{aligned} \alpha_i &\leftarrow \alpha_i+\eta\\ b &\leftarrow b+\eta y_i \end{aligned}\](4)转至(2),直至训练集中没有误分类点。
对偶形式中训练实例仅以內积的形式出现。为了方便,可以预先将训练集中实例间的內积计算出来并以矩阵的形式存储,这个矩阵就是所谓的\(\rm Gram\)矩阵:
\[\pmb G =[x_i \cdot x_j]_{N\times N }\]三、小结
从上述两种感知机学习算法中可以看出,对于线性可分的数据集,初值的选择与数据点选择的顺序都会影响最后参数的计算结果,同时也说明,感知机算法的结果不是唯一的,有无穷多解,这与初值的设定与数据点的选择顺序有关。对于线性不可分的数据集,在训练中会使得参数进行震荡,而不会收敛,所以感知机只能对线性可分的数据集进行二分类,若需要对非线性可分的数据集进行二分类,则需要用到支持向量机。