对于一幅图像,我们首先想到的图像特征就是图像边缘,图像边缘可以构造出这幅图像的轮廓,根据图像的轮廓我们可以大致获知图像的内容,这一过程可以抽象为将图像从面简化到线,从这个角度出发,我们可以尝试能否进一步将特征从线简化到点,使用这些特征点来表达图像的特征,进一步减少特征中的冗余信息。这种方法被称为角点检测法。
1. 角点
何为角点是我们首先要解决的问题,对于一幅图像来说,平坦区域(亮度变化平缓的区域)没有包含太多信息,不能作为图像的特征来与其他图像进行区别,因此边缘作为一个比较直观的特征可以与其他图像进行区别,进一步地在边缘处没有相交的点又相对比较平坦,由此可以得出边缘处相交的点可以作为图像特征,这些点即为角点,如下图所示为不同类型的角点。
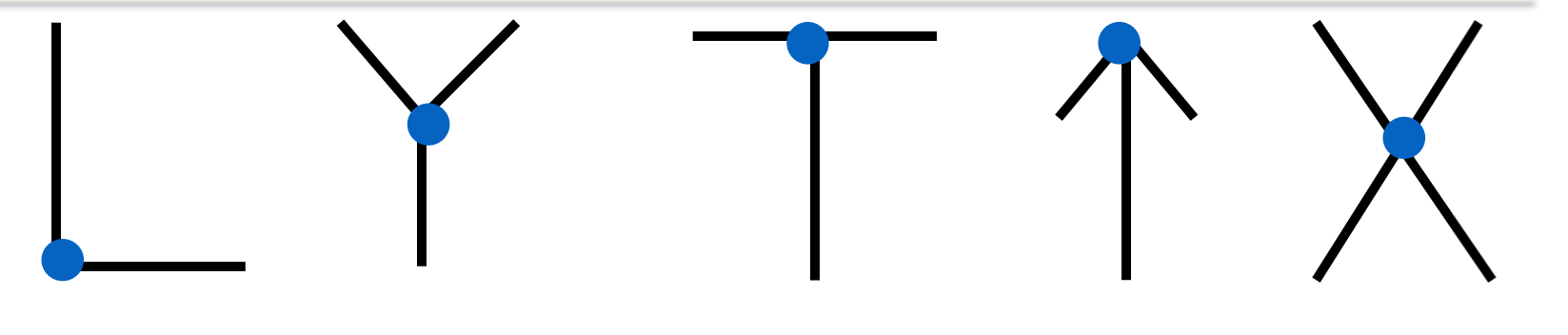
2. 角点检测的方法
角点检测主要有两种方法,Harris角点检测与FAST角点检测算法。
-
Harris角点检测算法
从角点的定义出发,可以看出角点所处位置与其他位置的不同之处是该位置向任意方向移动都会发生明显的灰度变化。在平坦区域处,向任意方向移动,灰度变化不明显,在边缘处,沿着边缘方向移动时,灰度变化不明显,在角点处,向任意方向移动,都会有明显的灰度变化,基于这个特点,可以实现角点检测。
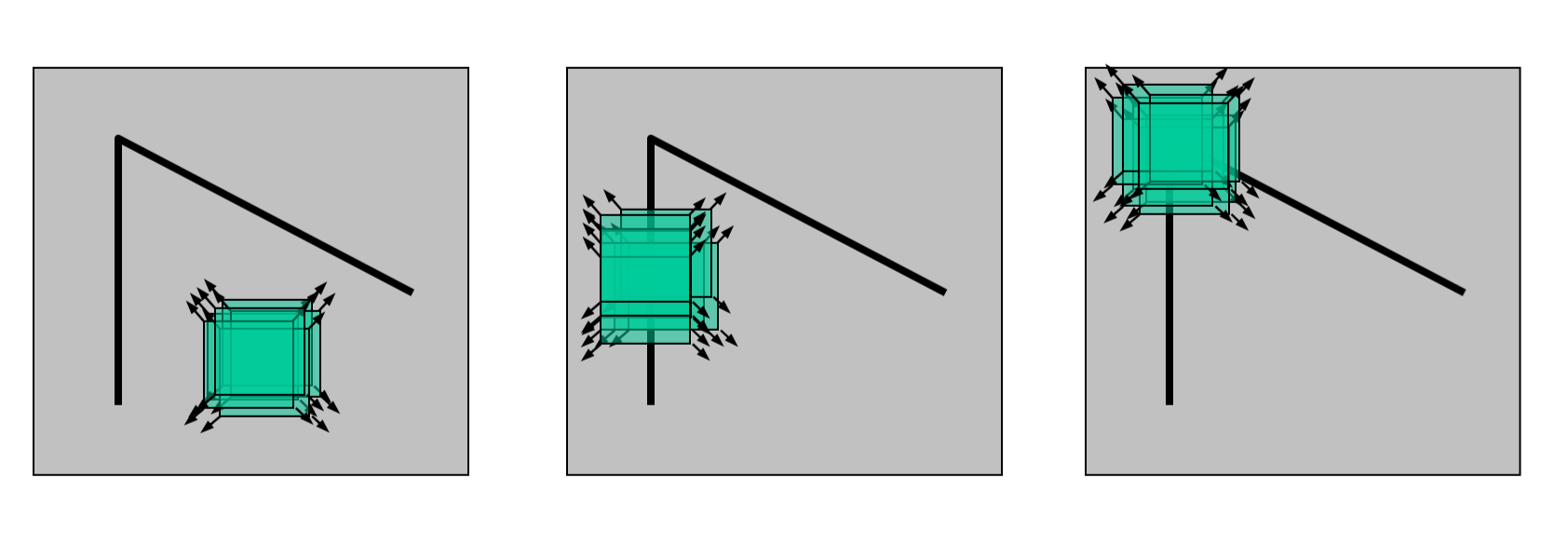
Harris角点检测的数学表达式为
\(E(u,v)=\sum_{x,y}w(x,y)\left[I(x+u,y+v)-I(x,y)\right]^2\) 其中\(u,v\)表示平移的移动量,\(x,y\)表示窗口内像素的坐标,\(w(x,y)\)表示窗口函数,可以所有权值为1,也可以使用一定的权重来分配窗口内不同的点,\(I(x+u,y+v)\)表示平移后的图像灰度,\(I(x,y)\)表示图像灰度。上式可以通过二元函数的泰勒展开进行化简即
\[I(x+u,y+v)\approx I(x,y)+uI_x+vI_y\]其中\(I_x,I_y\)分别为\(I(x,y)\)在\((x,y)\)处沿\(x,y\)方向的梯度,因此原式就可以化简为
\[\begin{aligned} E(u,v)&=\sum_{x,y}w(x,y)[uI_x+vI_y]^2\\ &=\sum_{x,y}w(x,y)(u^2I_x^2+2uvI_xI_y+v^2I_y^2)\\ &=\sum_{x,y}w(x,y)(u,v)\left(\begin{matrix} I_x^2&I_xI_y\\ I_xI_y&I_y^2 \end{matrix}\right) \left(\begin{matrix} u\\ v \end{matrix}\right) \end{aligned}\]令\(M=\sum_{x,y}w(x,y)\left(\begin{matrix}I_x^2&I_xI_y\\I_xI_y&I_y^2\end{matrix}\right)\),可以看出\(M\)矩阵是一个以\(I_x,I_y\)为变量的协方差矩阵,通过观察不同情况下的分布可以得出如下结论
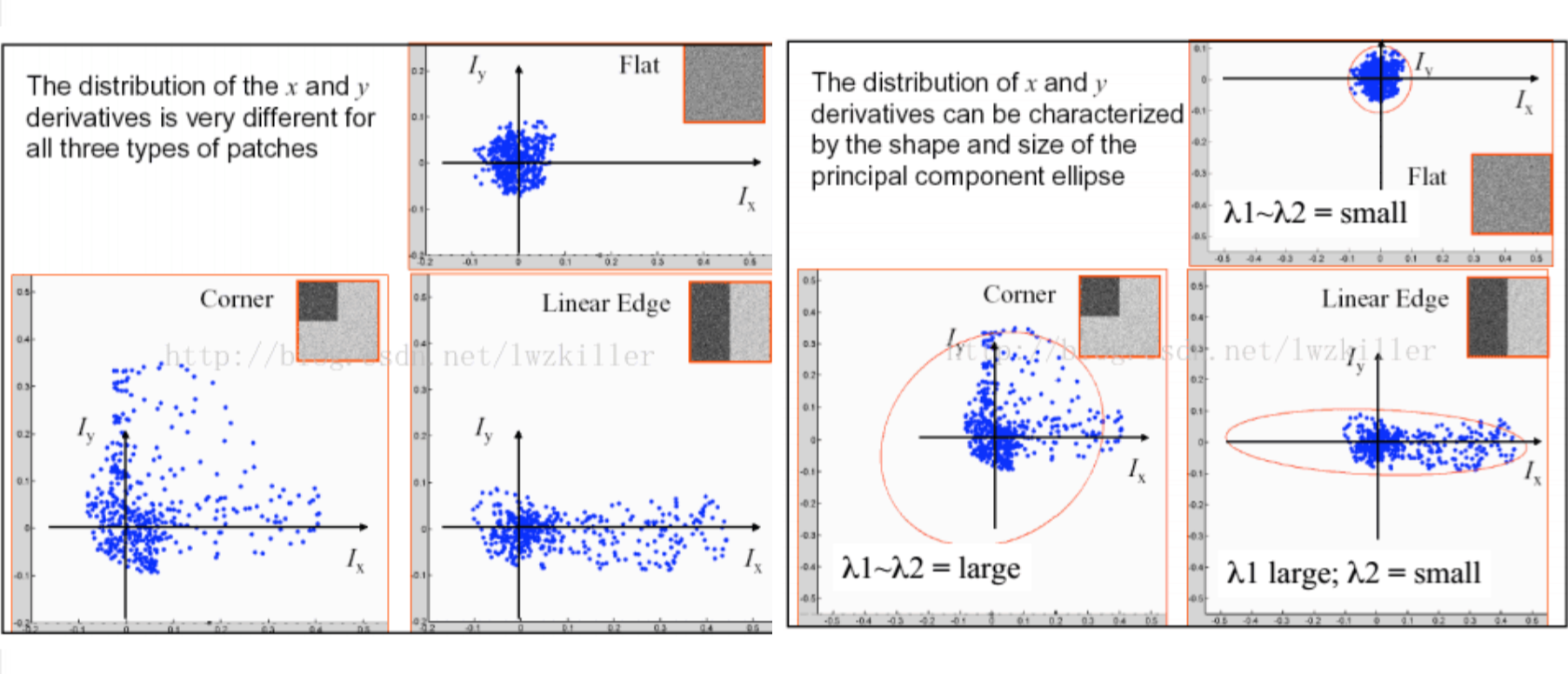
具体可以通过如下图来表示
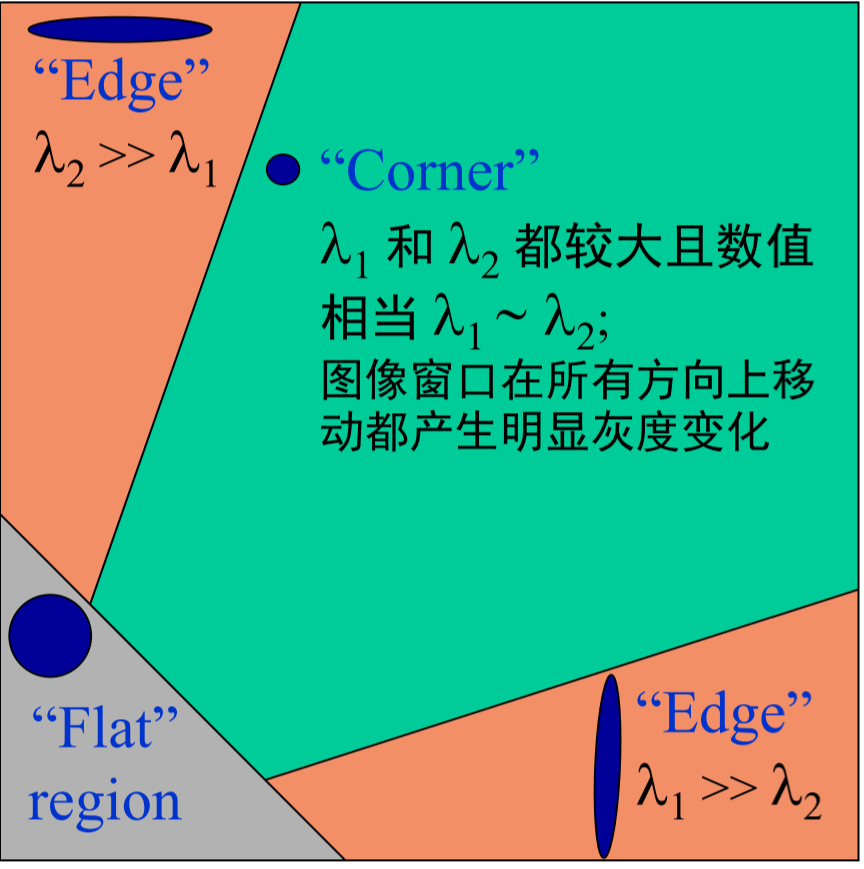
上图可以使用如下函数表达式来实现数学表达
\[R=det\ M-k(trace\ M)^2\]其中\(det\ M=\lambda_1\lambda_2,trace\ M=\lambda_1+\lambda_2\),\(k\)是超参数一般设置为0.04-0.06,根据实际使用进行调节。
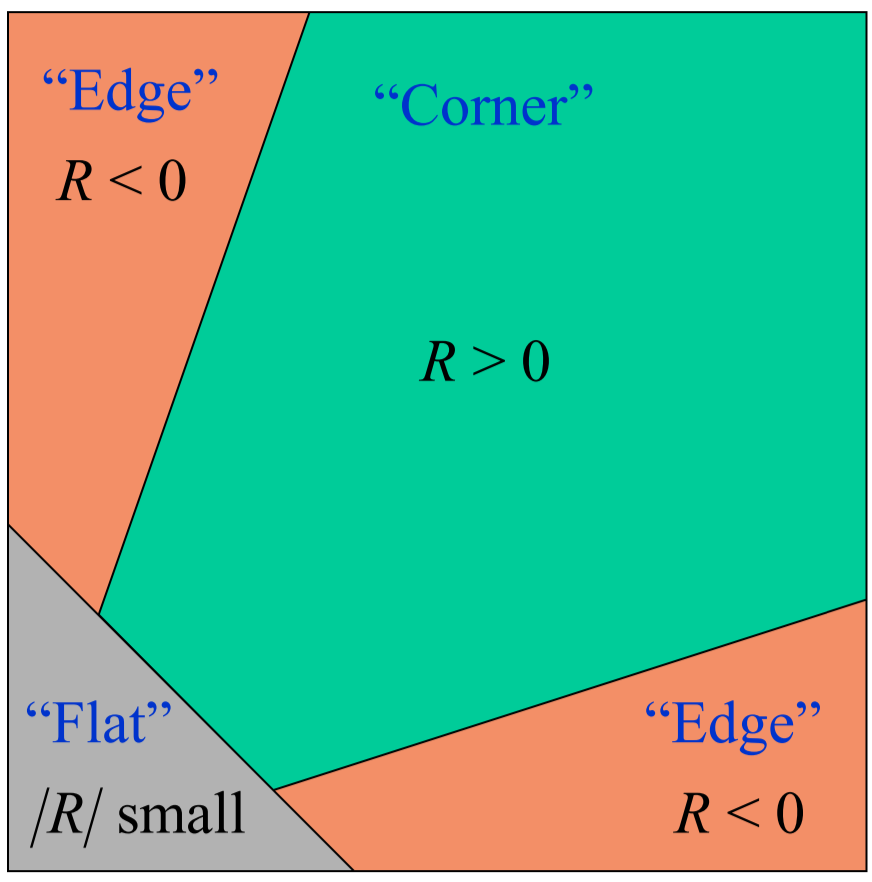
当\(\vert R\vert\)较小时,说明当前位置为平坦区域,当\(R<0\)时,说明当前位置处于边缘位置,当\(R>0\)且数值较大时,说明当前位置为角点。增大\(k\)值,会降低角点检测的灵敏度,反之则会增加角点检测的灵敏度。
-
FAST(Features from Accelerated Segment Test)
对于每一个像素,分别判断以该像素为中心的一个半径为3像素的离散化Bresenham圆,这个圆的边界上有16个像素,如果这个边界上有连续的n个像素都比中心像素点大于或小于一个阈值,则认为中心像素点是一个角点。