尺度不变特征转换(Scale Invariant Feature Transform, SIFT)算法顾名思义就是该算法提取的特征对尺度变化有不变性的特点,要理解这个算法,首先要理解尺度的概念,以及尺度不变性的定义。
1. 尺度不变性
对于平面直角坐标系来说,尺度可以表示为横纵坐标轴大的分度值,对于选择不同的分度值,我们得到的结果往往会有不同的结果,给我们直观的结果就是坐标系内的图像被放大或者缩小了。对于图像来说,尺度的变化就意味着,我们观察物体的位置距离物体的远近发生变化,这个距离的变化表现在图像上就是图像的清晰程度发生变化,即距离物体越近,我们得到的图像往往更加清晰,图像也比较大,距离越远,观察到的图像就会越模糊,图像也会比较小。
对于图像的模糊,Lindeberg等人已证明尺度归一化的LoG空间具有真正的尺度不变性,即\(\sigma^2\nabla^2 G\)算子具有尺度不变性,而DoG(高斯差分)可以近似表示该算子,因此可以使用DoG来近似实现尺度不变性。DoG函数为\(D(x,y,\sigma)=(G(x,y,k\sigma)-G(x,y,\sigma))*I(x,y)=L(x,y,k\sigma)-L(x,y,\sigma)\)。
2. SIFT算法
了解了尺度不变性后,可以进一步来看下SIFT算法的流程。
-
建立高斯差分金字塔
使用上下采样类模拟人眼观察物体近大远小的特点,使用高斯差分算子来模糊图像。可以得到如下的高斯金字塔。
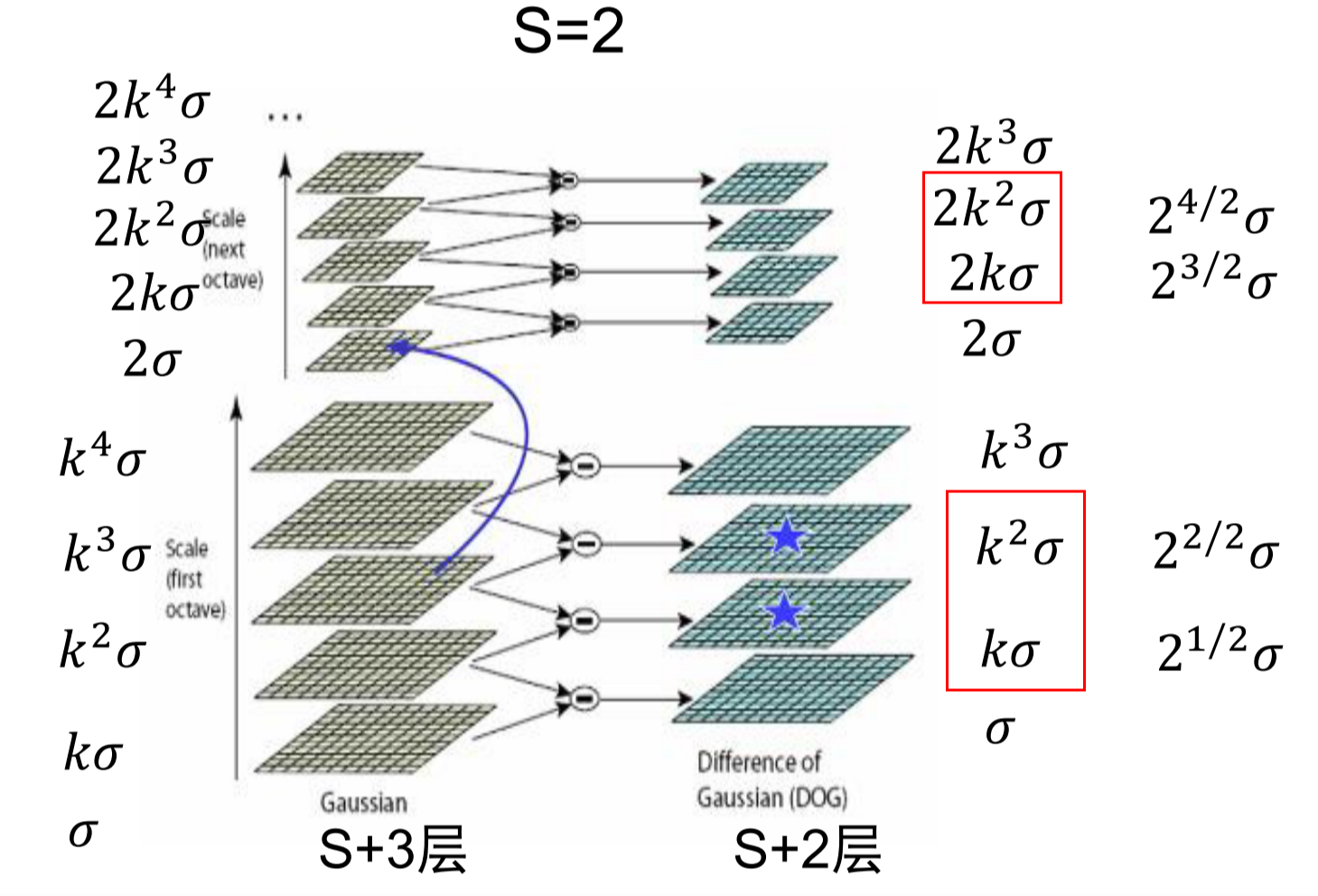
使用不同的高斯核模糊图像,然后将相邻的两个差分得到DoG尺度空间的图像。下一层使用上一层倒数第三个图像下采样两倍得到。
-
确定极值点
DoG尺度空间是一个三维空间\(x,y,\sigma\),要在三个空间即周围26个点都是极值点才能判断该点为极值点。在DoG空间中寻找极值点时,只能在中间,不能在两边,所以当提取特征点的层数为S时,DoG尺度空间为S+2。
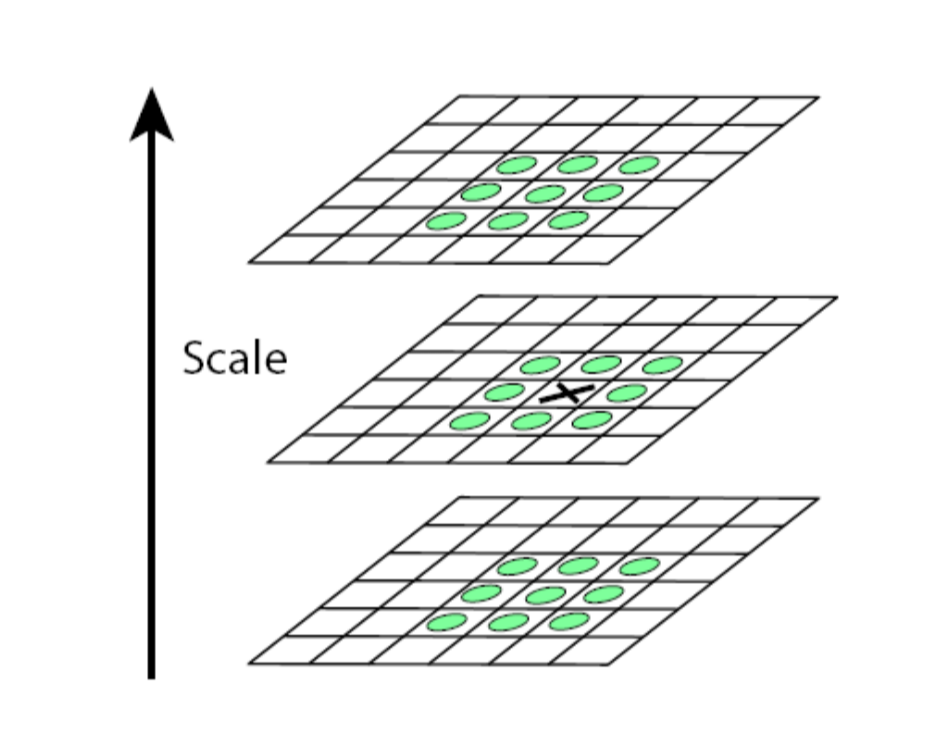
以上得到的极值点不一定是真实空间的极值点,因为上述图像中的点都是离散采样得到的,因此可以通过对这些点进行曲线拟合,计算极值点,实现关键点的精确定位。
对DoG函数进行二级泰勒展开可得,\(D(x)=D+\frac{\partial D^T}{\partial x}x+\frac{1}{2}x^T\frac{\partial^2D}{\partial x^2}x\),可以得到偏移量\(\hat x=-\frac{\partial^2D^{-1}}{\partial x^2}\frac{\partial D}{\partial x}\),其中\(\hat x=(\hat x,\hat y,\hat \sigma)\),中的任意一个偏移量大于0.5说明精确极值点更接近另一个临近点,改变关键点位置重新计算。
同时还要去除不稳定的关键点,首先是对比度较低的点\(\vert D(\hat x)\vert <0.03\)。其次是边缘上的点,使用Hessian矩阵进行判别,Hessian矩阵表示为
\[H=\left[\begin{matrix} D_{xx}&D_{xy}\\ D_{xy}&D_{yy} \end{matrix} \right]\]令其特征值之间的关系为\(\lambda_1=r\lambda_2\)使用\(\frac{Tr^2(H)}{Det(H)}=\frac{(\lambda_1+\lambda_2)^2}{\lambda_1\lambda_2}=\frac{(r+1)^2}{r}>\frac{(T_r+1)^2}{T_r}\)判断关键点是否为边缘上的点,\(T_r\)为超参数,可以设定为10。
- 确定关键点的主方向
以特征点为中心,以\(3\times 1.5\sigma\)为半径,计算这个范围内所有点的梯度幅值与幅角。构建这个区域内的梯度方向直方图,直方图每36度为一个bin,然后一共分为10个bin。同时为了避免图像仿射变化对特征点的影响,使用高斯函数对梯度幅值进行平滑,即对梯度幅值进行加权,距离特征点越近的点对梯度方向的贡献越大。根据以此构建出的梯度直方图找到其峰值点设为主方向,超过主峰值80%的,且是局部极值点的设为辅助方向,一个特征点可能产生多个坐标、尺度相同,但方向不同的特征点。多方向的处理方法可以降低噪声的影响,提升算法的鲁棒性。
-
构造描述子
描述子就是对特征的描述,实例化就是特征向量,特征向量可以实现对特征的区别,即根据特征向量对特征的描述,我们可以判断出特征点的区别,这就是描述子。
为了保证SIFT算法的旋转不变性,根据刚才求得的特征的主方向,将图像旋转到特征的主方向上,这样对于不同的方向的图像,虽然图像整体发生了旋转,同一个特征点位置的方向不同,但是特征点周围点相对于主方向的位置是不变的,因此可以利用这个特点实现特征点的旋转不变性。
由于计算机是二进制,为了方便存储,在构建SIFT描述子时每个子区域的梯度方向分为8个bin,每个bin的宽度为45度。直方图的值为梯度幅值高斯函数的加权累加。
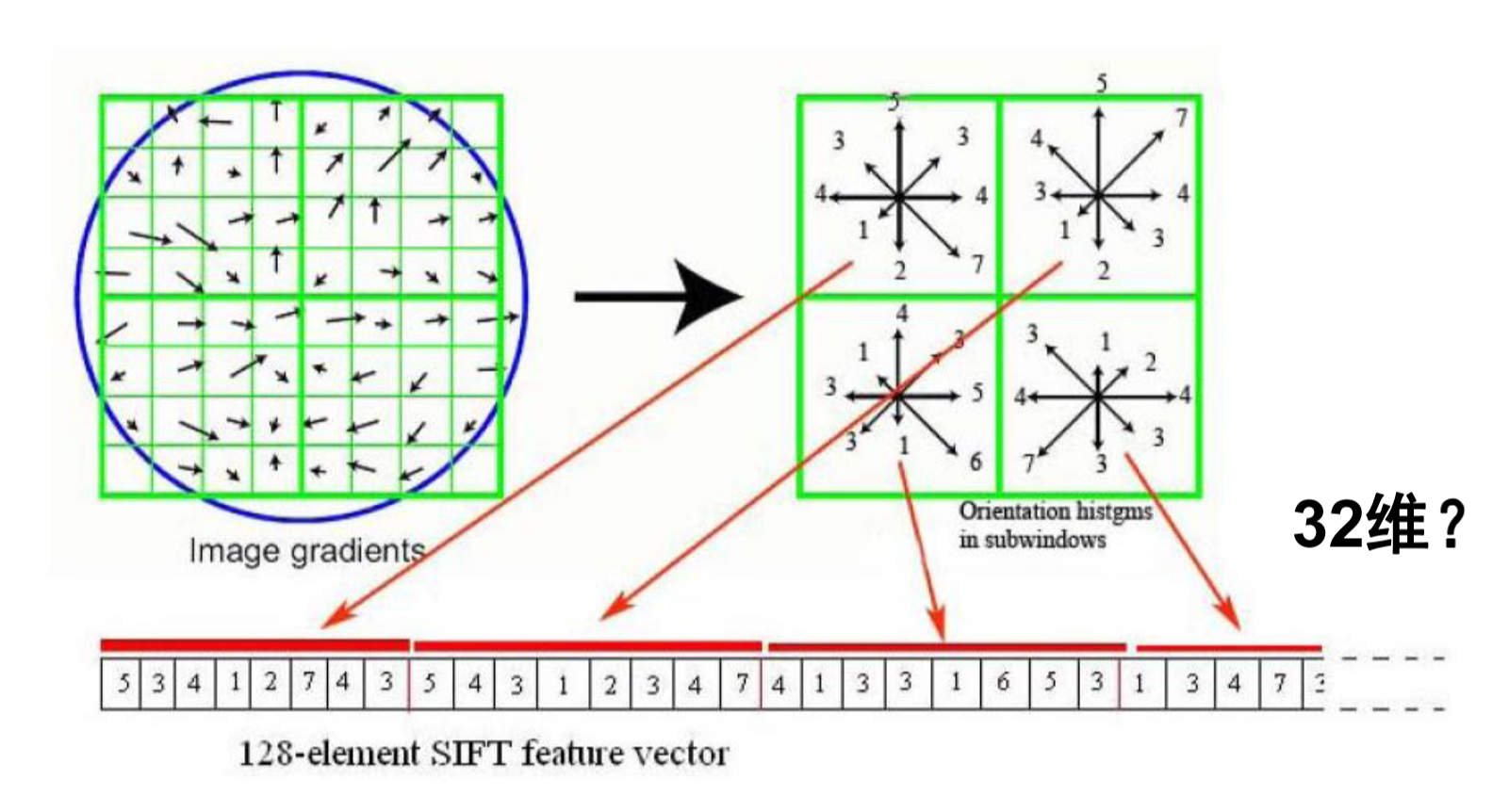
至此SIFT算法完成了对特征点的提取与描述子的构建。